Binary Search Tree


Apa itu binary search tree?

Binary search tree adalah suatu data struktur yang menyerupai pohon. Dari kata binary, kita bisa menyimpulkan bahwa pohon tersebut hanya memiliki maksimal 2 cabang.

Oleh karena itu, ia bukan merupakan tree karena tree bisa memiliki lebih dari dua cabang. Ia pun juga berbeda dari binary tree biasa, yang kita bisa lihat dari struktur kode insertion dan deletion yang nanti kita aplikasikan.

Binary search tree ini harus kita kuasai terlebih dahulu sebelum kita mengenal varian binary tree yang lebih banyak lagi, seperti AVL tree, Red Black Tree, dan kawan-kawannya.  

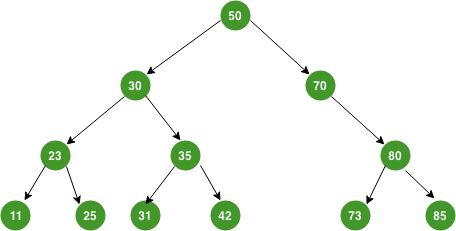
Gambar binary search tree:


Sumber: https://algorithmtutor.com/images/BinarySearchTrees.png

Binary search tree memiliki struktur umum sebagai berikut:
struct Node{
               int value;
               struct Node* right;
               struct Node* left;
} typedef Node;
Node* head;

Ciri khas yang bisa kita lihat dari gambar di atas adalah:
  • Cabang kiri memiliki value yang lebih kecil daripada parentnya
  • Cabang kanan memiliki value yang lebih besar daripada parentnya
Kita bisa melakukan operasi-operasi ini di dalam binary tree:
  • Insertion
  • Deletion
  • Searching

Perlu diingat, semua proses ini dilakukan dengan melakukan recursion, karena hal tersebut akan sulit dilakukan jika kita memakai teknik pengulangan biasa (for, while, do while).

Insertion di dalam binary search tree ini memiliki ciri khas sebagai berikut:
  • Jika value yang ingin kita insert lebih besar daripada parentnya, maka kita akan melangkah ke cabang kanan
  • Jika value yang ingin kita insert lebih kecil daripada parentnya, maka kita akan melangkah ke cabang kiri
  • Hal ini terus kita ulang hingga ketemu dengan node null.
Cara searching binary search tree dibagi menjadi 3:
=======================================
Semua teknik searching ini…
  • Dimulai dari node paling atas terlebih dahulu
  • Proses rekursif terus berjalan hingga ketemu null
  • Dinamakan Depth-First-Search

=======================================
Inorder traversal:
  1. Kita Melangkah dari node parent ke cabang kiri
  2. print value dari node tersebut
  3. Lanjut melangkah ke cabang kanan

Preorder traversal:
  1. print value dari node tersebut
  2. Kita Melangkah ke cabang kiri
  3. Lanjut melangkah ke cabang kanan

Postorder traversal:
  1. Kita Melangkah ke cabang kiri
  2. Lanjut melangkah ke cabang kanan
  3. Terakhir, print value dari node tersebut


Deletion di dalam binary search tree ini memiliki ciri khas sebagai berikut:
--- Proses awal sama seperti insertion---
  • Jika value yang ingin kita insert lebih besar daripada parentnya, maka kita akan melangkah ke cabang kanan
  • Jika value yang ingin kita insert lebih kecil daripada parentnya, maka kita akan melangkah ke cabang kiri
  • Hal ini terus kita ulang hingga ketemu dengan value yang sama atau value yang kita cari tidak ada alias null.

--- Proses kedua dan jika valuenya ada---
  • Tidak punya anak sama sekali: Tinggal hapus saja node tersebut.
  • Dengan kondisi 1 anak saja: Kita copy value dari anak kiri atau kanan lalu menghapusnya.
  • Dengan kondisi 2 anak: 
          Anda memiliki 2 pilihan langkah:
  1.  Langkah ke kiri sekali terlebih dahulu dan terus melangkah ke kanan sampai ketemu node null
  2.  Langkah ke kanan sekali terlebih dahulu dan terus melangkah ke kiri sampai ketemu node null
  3.  Setelah itu, kita tinggal copy value dari node tersebut, lalu kita menghapus node tersebut

Berikut adalah contoh implementasi binary search tree dalam bentuk aplikasi sederhana:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

struct Node{
               char name[100];
               int age;
               unsigned long long int nameInASCII;
               struct Node* right;
               struct Node* left;
} typedef Node;

Node* head = NULL;
Node* temp = NULL;

unsigned long long int giveASCIILength(char nameNew[]){
               int index = 0;
               unsigned long long int asciiLength = 0;
               for (index; nameNew[index] != '\0'; index++){
                              asciiLength += nameNew[index];
               }
               return asciiLength;
}

Node* oneNode(int ageNew, char nameNew[100]){
               temp = (Node*) malloc(sizeof(Node));
               temp->age = ageNew;
               strcpy(temp->name, nameNew);
               temp->nameInASCII = giveASCIILength(nameNew);
               temp->left = NULL;
               temp->right = NULL;
               return temp;
}

int tempNumber = 0;
unsigned long long int tempLongNumber = 0;
char tempSentence[100] = {};
int length = 0;
int age = 0;
char tempName[100] = {};

void printLine(char message[]){
               printf("%s\n", message);
}

int giveRangedNumber(int min, int max, char message[]){
               do{
                              printf("%s ", message);
                              scanf("%i", &tempNumber);
                              getchar();           
               }while(tempNumber < min || tempNumber > max);
               return tempNumber;
}
char* giveRangedSentenceLength(int min, int max, char message[]){
               do{
                              printf("%s ", message);
                              scanf("%[^\n]", tempSentence);
                              getchar();
                              length = strlen(tempSentence);
               }while(length < min || length > max);
               return tempSentence;
}

void printContents(Node* node){
               printLine("=========================");
               printf("Name: %s\n", node->name);
               printf("ASCII value: %llu\n", node->nameInASCII);
               printf("Age: %i\n", node->age);
               printLine("=========================");
               printLine("");
}

void inorderTraversal(Node* current){
               if (current != NULL){
                              inorderTraversal(current->left);
                              printContents(current);
                              inorderTraversal(current->right);
               }
}
void preorderTraversal(Node* current){
               if (current != NULL){
                              printContents(current);
                              inorderTraversal(current->left);
                              inorderTraversal(current->right);
               }
}
void postorderTraversal(Node* current){
               if (current != NULL){
                              inorderTraversal(current->left);
                              inorderTraversal(current->right);
                              printContents(current);
               }
}
void searchOperations(){
               int choice = 0;
               do{
                              system("cls");
                              printLine("Search operation:");
                              printLine("1. Inorder Traversal");
                              printLine("2. Preorder Traversal");
                              printLine("3. Postorder Traversal");
                              printLine("4. Back");
                              printLine("If there are no data to be displayed, it means that your content is still empty!");
                              choice = giveRangedNumber(1, 4, "Choose:");
                              if (choice == 1){
                                             inorderTraversal(head);
                                             printLine("Done searching!");
                                             getchar();
                              }
                              else if (choice == 2){
                                             preorderTraversal(head);
                                             printLine("Done searching!");
                                             getchar();
                              }
                              else if (choice == 3){
                                             postorderTraversal(head);
                                             printLine("Done searching!");
                                             getchar();
                              }
               }while(choice != 4);
}

Node* insertBST(Node* newNode, Node* curr){
               if (head == NULL){
                              head = newNode;
                              return head;
               }
               else if (curr != NULL){
                              if (newNode->nameInASCII < curr->nameInASCII){
                                             curr->left = insertBST(newNode, curr->left);
                              }
                              else if (newNode->nameInASCII > curr->nameInASCII){
                                             curr->right = insertBST(newNode, curr->right);
                              }
                              else{
                                             printLine("A data has the same ASCII value. Cannot be inserted!");
                              }
               }
               else{
                              curr = newNode;
               }
               return curr;
}
Node* deleteData(Node* current, unsigned long long int asciiValue){
               if (head == NULL){
                              printLine("We cannot delete the data because the name does not exist!");
                              getchar();
                              return NULL;
               }
               else if (current == NULL){
                              printLine("We could not find the data you requested! Try rechecking your spelling and type again!");
                              getchar();
               }
               else if (asciiValue < current->nameInASCII){
                              current->left = deleteData(current->left, asciiValue);
               }
               else if (asciiValue > current->nameInASCII){
                              current->right = deleteData(current->right, asciiValue);
               }
               else{
                              // Found the data!
                              if (current->left == NULL && current->right == NULL){
                                             // No children at all
                                             free(current);
                                             return NULL;
                              }
                              else if (current->left == NULL){
                                             // if we want to traverse left-right but there is no value on the left
                                             strcpy(current->name, current->right->name);
                                             current->nameInASCII = current->right->nameInASCII;
                                             current->age = current->right->age;
                                             free(current->right);
                                             current->right = NULL;
                              }
                              else{
                                             temp = current->left;
                                             while(temp->right->right != NULL){
                                                            printf("Reached here!");
                                                            temp = temp->right;
                                             }
                                             strcpy(current->name, temp->right->name);
                                             current->nameInASCII = temp->right->nameInASCII;
                                             current->age = temp->right->age;
                                             free(temp->right);
                                             temp->right = NULL;
                              }
               }
               return current;
}
void mainMenu(){
               int choice = 0;
               do{
                              system("cls");
                              printLine("Welcome to Binary Search Tree program!");
                              printLine("Please choose what to do:");
                              printLine("1. Insert data");
                              printLine("2. Delete data");
                              printLine("3. Search");
                              printLine("4. Exit");
                              choice = giveRangedNumber(1, 5, "Choose: ");
                              if (choice == 1){
                                             printLine("====This will sort the data by ASCII values====");
                                             age = giveRangedNumber(1, 99, "Please enter the age[1-99]:");
                                             strcpy(tempName, giveRangedSentenceLength(10, 100, "Please enter the name [10-100]:"));
                                             head = insertBST(oneNode(age, tempName), head);
                                             printLine("Your data has been inserted!");
                                             getchar();
                              }
                              else if (choice == 2){
                                             strcpy(tempName, giveRangedSentenceLength(10, 100, "Please enter the name to be deleted[10-100]:"));
                                             tempLongNumber = giveASCIILength(tempName);
                                             head = deleteData(head, tempLongNumber);
                              }
                              else if (choice == 3){
                                             searchOperations();
                              }
                              else if (choice == 4){
                                             printLine("Thank you for using my app! :) :) :)");
                              }
               }while(choice != 4);
}

int main(){
               mainMenu();
               return 0;
}

Tips: jika anda ingin mengetahui benarnya program Anda berjalan, Anda bisa menggunakan opsi inorder traversal. Jika benar, Anda bisa lihat bahwa data ASCII value yang ditampilkan mulai dari paling rendah ke paling besar.

Worst case time complexity untuk binary search tree bisa mencapai jumlah height / ketinggiannya jika kondisi cabangnya menumpuk ke kiri atau ke kanan. Oleh karena itu, kita akan membahas AVL tree agar kita bisa bermain dengan ketinggian di tree agar mencapai time complexity minimal dalam blog mendatang.

Happy Coding!


Comments

Post a Comment

Popular posts from this blog

Heap

Image
Halo semuanya, setelah kita belajar macam-macam balancing tree (AVL Tree, Red Black Tree, dan B-Tree), maka sekarang kita akan belajar tree yang direpresentasikan dalam bentuk array, yaitu heap. Apa itu heap? Heap adalah salah satu varian dari binary tree, namun Ia memiliki prinsip dan aturan sebagai berikut: Heap adalah binary tree yang direpresentasikan dalam bentuk array. Untuk melakukan traverse node dari heap, kita tidak menggunakan cara recursive, namun menggunakan proses iteratif. Berikut ini adalah contoh gambar dari heap: Sumber:   https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Max-Heap.svg/1200px-Max-Heap.svg.png Jika direpresentasikan dalam bentuk array, maka terlihat sebagai berikut: Index 0 1 2 3 4 5 6 7 8 Value 100 19 36 17 3 25 1 2 7 Catatan: Heap selalu berupa balanced binary tree. Heap ini memiliki 3 varian, yaitu...
Read more

AVL Tree

Image
AVL Tree AVL Tree secara dasarnya sama seperti Binary Search Tree yang umumnya, namun tree ini memiliki perbedaan-perbedaan yang mendasar: Bisa dibilang bahwa tree ini hampir selalu berupa perfect binary tree. Hal ini terjadi karena AVL Tree mengoptimasi cabang-cabang anakannya sehingga cabangnya tidak terlalu ke kiri atau ke kanan Akibatnya, perbedaan ketinggian pada setiap cabang yang terdapat di tree ini tidak boleh lebih dari 1. Inilah yang kita sebut sebagai Balanced Binary Tree. Berikut ini adalah contoh perbandingan gambar AVL Tree dan yang bukan: Kiri – Bukan AVL Tree karena perbedaan ketinggian di node 8 dan 18 lebih dari 1, namun gambar kanan memenuhi persyaratan AVL Tree Sumber: https://www.geeksforgeeks.org/avl-tree-set-1-insertion/ Mengapa AVL Tree perlu dipakai? Bayangkan jika kita menggunakan binary search tree. Jika kita lihat, anakan yang lebih besar dari parentnya, maka nodenya ditaruh di kanan dan sebaliknya. Bagaimana jika data ya...
Read more

Binary Tree dan Hash Table

Image
Hash Table Apa itu hash table? Hash table adalah suatu tipe data structure yang meliputi: Array Linked List Bentuk umum hash table dalam bahasa C: Struct Node{                int data;                Node* left;                Node* right; } Struct HashTable{                Node* head;                Node* tail; } HashTable hash[10]; // Tentukan array sizenya terlebih dahulu Nah, suatu data ini bisa masuk ke suatu index dalam array dengan menggunakan rumus sebagai berikut: Size of array: bilangan % arraySize. Misal angka bilangan di dalam suatu data adalah 10 dan arraySize adalah 13, maka Ia aka...
Read more