AVL Tree


AVL Tree
AVL Tree secara dasarnya sama seperti Binary Search Tree yang umumnya, namun tree ini memiliki perbedaan-perbedaan yang mendasar:
  • Bisa dibilang bahwa tree ini hampir selalu berupa perfect binary tree. Hal ini terjadi karena AVL Tree mengoptimasi cabang-cabang anakannya sehingga cabangnya tidak terlalu ke kiri atau ke kanan
  • Akibatnya, perbedaan ketinggian pada setiap cabang yang terdapat di tree ini tidak boleh lebih dari 1. Inilah yang kita sebut sebagai Balanced Binary Tree.
Berikut ini adalah contoh perbandingan gambar AVL Tree dan yang bukan:

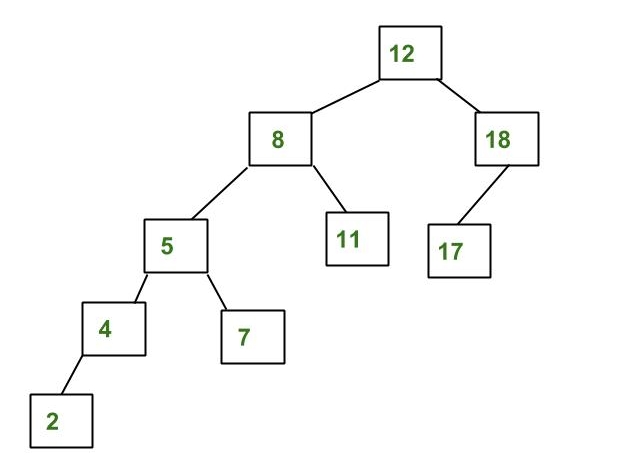
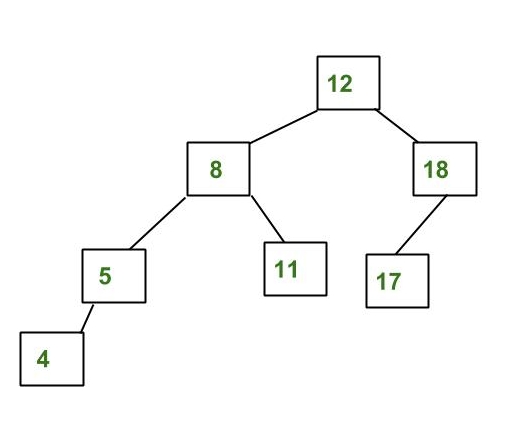
Kiri – Bukan AVL Tree karena perbedaan ketinggian di node 8 dan 18 lebih dari 1, namun gambar kanan memenuhi persyaratan AVL Tree
Sumber: https://www.geeksforgeeks.org/avl-tree-set-1-insertion/

Mengapa AVL Tree perlu dipakai?
Bayangkan jika kita menggunakan binary search tree. Jika kita lihat, anakan yang lebih besar dari parentnya, maka nodenya ditaruh di kanan dan sebaliknya. Bagaimana jika data yang diinsert selalu lebih besar dari parentnya atau sebaliknya? Otomatis, BST ini akan menjadi skewed binary tree, dimana perbedaan ketinggian ini bahkan bisa setara dengan jumlah node di tree tersebut. Alhasil, proses insertion, deletion, dan searching bisa sama seperti linked list biasa. Oleh karena itu, itulah sebabnya AVL Tree diperlukan untuk memecahkan kasus ini.
Untuk menyeimbangkan tree ini, maka diperlukan yang namanya left and right rotation.

Syarat-syarat Balanced Binary Tree: jika pebedaan ketinggian antar anakan node <= 1.

Untuk proses insertion, deletion, dan searching sama seperti binary search tree pada umumnya. Namun, di akhir operasi tersebut, Ia mentraverse up untuk mengecek apakah node tersebut menyalahi aturan Balanced Binary Tree.

Macam-macam bentuk rotation:
·        Single Rotation (left-left atau right right):
Sumber: https://sikisik.wordpress.com/struktur-data/
Pada contoh diatas termasuk left rotation, karena dari 30 ke 22 ke kiri, dan dari 22 ke 15 ke kiri juga.

·        Double Rotation (left – right atau right - left):
Sumber: https://sikisik.wordpress.com/struktur-data/

Rotasi pertama: Left - right

Sumber: https://sikisik.wordpress.com/struktur-data/
Rotasi kedua: left-left

Contoh implementasi AVL Tree (insertion):
// C++ program to insert a node in AVL tree 
#include<bits/stdc++.h>
using namespace std;
  
// An AVL tree node 
class Node 
{ 
    public:
    int key; 
    Node *left; 
    Node *right; 
    int height; 
}; 
  
// A utility function to get maximum
// of two integers 
int max(int a, int b); 
  
// A utility function to get the 
// height of the tree 
int height(Node *N) 
{ 
    if (N == NULL) 
        return 0; 
    return N->height; 
} 
  
// A utility function to get maximum
// of two integers 
int max(int a, int b) 
{ 
    return (a > b)? a : b; 
} 
  
/* Helper function that allocates a 
   new node with the given key and 
   NULL left and right pointers. */
Node* newNode(int key) 
{ 
    Node* node = new Node();
    node->key = key; 
    node->left = NULL; 
    node->right = NULL; 
    node->height = 1; // new node is initially
                      // added at leaf 
    return(node); 
} 
  
// A utility function to right
// rotate subtree rooted with y 
// See the diagram given above. 
Node *rightRotate(Node *y) 
{ 
    Node *x = y->left; 
    Node *T2 = x->right; 
  
    // Perform rotation 
    x->right = y; 
    y->left = T2; 
  
    // Update heights 
    y->height = max(height(y->left),
                    height(y->right)) + 1; 
    x->height = max(height(x->left),
                    height(x->right)) + 1; 
  
    // Return new root 
    return x; 
} 
  
// A utility function to left 
// rotate subtree rooted with x 
// See the diagram given above. 
Node *leftRotate(Node *x) 
{ 
    Node *y = x->right; 
    Node *T2 = y->left; 
  
    // Perform rotation 
    y->left = x; 
    x->right = T2; 
  
    // Update heights 
    x->height = max(height(x->left),    
                    height(x->right)) + 1; 
    y->height = max(height(y->left), 
                    height(y->right)) + 1; 
  
    // Return new root 
    return y; 
} 
  
// Get Balance factor of node N 
int getBalance(Node *N) 
{ 
    if (N == NULL) 
        return 0; 
    return height(N->left) - height(N->right); 
} 
  
// Recursive function to insert a key
// in the subtree rooted with node and
// returns the new root of the subtree. 
Node* insert(Node* node, int key) 
{ 
    /* 1. Perform the normal BST insertion */
    if (node == NULL) 
        return(newNode(key)); 
  
    if (key < node->key) 
        node->left = insert(node->left, key); 
    else if (key > node->key) 
        node->right = insert(node->right, key); 
    else // Equal keys are not allowed in BST 
        return node; 
  
    /* 2. Update height of this ancestor node */
    node->height = 1 + max(height(node->left), 
                        height(node->right)); 
  
    /* 3. Get the balance factor of this ancestor 
        node to check whether this node became 
        unbalanced */
    int balance = getBalance(node); 
  
    // If this node becomes unbalanced, then 
    // there are 4 cases 
  
    // Left Left Case 
    if (balance > 1 && key < node->left->key) 
        return rightRotate(node); 
  
    // Right Right Case 
    if (balance < -1 && key > node->right->key) 
        return leftRotate(node); 
  
    // Left Right Case 
    if (balance > 1 && key > node->left->key) 
    { 
        node->left = leftRotate(node->left); 
        return rightRotate(node); 
    } 
  
    // Right Left Case 
    if (balance < -1 && key < node->right->key) 
    { 
        node->right = rightRotate(node->right); 
        return leftRotate(node); 
    } 
  
    /* return the (unchanged) node pointer */
    return node; 
} 

Node* deleteNode(Node* root, int key) 
{ 
      
    // STEP 1: PERFORM STANDARD BST DELETE 
    if (root == NULL) 
        return root; 
  
    // If the key to be deleted is smaller 
    // than the root's key, then it lies
    // in left subtree 
    if ( key < root->key ) 
        root->left = deleteNode(root->left, key); 
  
    // If the key to be deleted is greater 
    // than the root's key, then it lies 
    // in right subtree 
    else if( key > root->key ) 
        root->right = deleteNode(root->right, key); 
  
    // if key is same as root's key, then 
    // This is the node to be deleted 
    else
    { 
        // node with only one child or no child 
        if( (root->left == NULL) ||
            (root->right == NULL) ) 
        { 
            Node *temp = root->left ? 
                         root->left : 
                         root->right; 
  
            // No child case 
            if (temp == NULL) 
            { 
                temp = root; 
                root = NULL; 
            } 
            else // One child case 
            *root = *temp; // Copy the contents of 
                           // the non-empty child 
            free(temp); 
        } 
        else
        { 
            // node with two children: Get the inorder 
            // successor (smallest in the right subtree) 
            Node* temp = minValueNode(root->right); 
  
            // Copy the inorder successor's 
            // data to this node 
            root->key = temp->key; 
  
            // Delete the inorder successor 
            root->right = deleteNode(root->right, 
                                     temp->key); 
        } 
    } 
  
    // If the tree had only one node
    // then return 
    if (root == NULL) 
    return root; 
  
    // STEP 2: UPDATE HEIGHT OF THE CURRENT NODE 
    root->height = 1 + max(height(root->left), 
                           height(root->right)); 
  
    // STEP 3: GET THE BALANCE FACTOR OF 
    // THIS NODE (to check whether this 
    // node became unbalanced) 
    int balance = getBalance(root); 
  
    // If this node becomes unbalanced, 
    // then there are 4 cases 
  
    // Left Left Case 
    if (balance > 1 && 
        getBalance(root->left) >= 0) 
        return rightRotate(root); 
  
    // Left Right Case 
    if (balance > 1 && 
        getBalance(root->left) < 0) 
    { 
        root->left = leftRotate(root->left); 
        return rightRotate(root); 
    } 
  
    // Right Right Case 
    if (balance < -1 && 
        getBalance(root->right) <= 0) 
        return leftRotate(root); 
  
    // Right Left Case 
    if (balance < -1 && 
        getBalance(root->right) > 0) 
    { 
        root->right = rightRotate(root->right); 
        return leftRotate(root); 
    } 
  
    return root; 
} 


// A utility function to print preorder 
// traversal of the tree. 
// The function also prints height 
// of every node 
void preOrder(Node *root) 
{ 
    if(root != NULL) 
    { 
        cout << root->key << " "; 
        preOrder(root->left); 
        preOrder(root->right); 
    } 
} 
  
// Driver Code
int main() 
{ 
    Node *root = NULL; 
      
    /* Constructing tree given in 
    the above figure */
    root = insert(root, 10); 
    root = insert(root, 20); 
    root = insert(root, 30); 
    root = insert(root, 40); 
    root = insert(root, 50); 
    root = insert(root, 25); 
    root = deleteNode(root, 20);
    root = deleteNode(root, 50);
    cout << "Preorder traversal of the "
            "constructed AVL tree is \n"; 
    preOrder(root); 
      
    return 0; 
} 

Source code:
·        https://www.geeksforgeeks.org/avl-tree-set-1-insertion/
·        https://www.geeksforgeeks.org/avl-tree-set-2-deletion/
Untuk AVL Tree, Ia sebaiknya digunakan apabila proses insertion dan deletion tidak terlalu banyak. Bisa jadi pada saat insertion atau deletion, Ia membutuhkan lebih dari satu rotasi. Itulah sebabnya, AVL Tree lebih digunakan untuk proses searching yang lebih sering. Jika Anda ingin melakukan proses insertion dan deletion yang lebih sering, gunakanlah Red Black Tree.

Comments

Post a Comment

Popular posts from this blog

Heap

Image
Halo semuanya, setelah kita belajar macam-macam balancing tree (AVL Tree, Red Black Tree, dan B-Tree), maka sekarang kita akan belajar tree yang direpresentasikan dalam bentuk array, yaitu heap. Apa itu heap? Heap adalah salah satu varian dari binary tree, namun Ia memiliki prinsip dan aturan sebagai berikut: Heap adalah binary tree yang direpresentasikan dalam bentuk array. Untuk melakukan traverse node dari heap, kita tidak menggunakan cara recursive, namun menggunakan proses iteratif. Berikut ini adalah contoh gambar dari heap: Sumber:   https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Max-Heap.svg/1200px-Max-Heap.svg.png Jika direpresentasikan dalam bentuk array, maka terlihat sebagai berikut: Index 0 1 2 3 4 5 6 7 8 Value 100 19 36 17 3 25 1 2 7 Catatan: Heap selalu berupa balanced binary tree. Heap ini memiliki 3 varian, yaitu...
Read more

Binary Tree dan Hash Table

Image
Hash Table Apa itu hash table? Hash table adalah suatu tipe data structure yang meliputi: Array Linked List Bentuk umum hash table dalam bahasa C: Struct Node{                int data;                Node* left;                Node* right; } Struct HashTable{                Node* head;                Node* tail; } HashTable hash[10]; // Tentukan array sizenya terlebih dahulu Nah, suatu data ini bisa masuk ke suatu index dalam array dengan menggunakan rumus sebagai berikut: Size of array: bilangan % arraySize. Misal angka bilangan di dalam suatu data adalah 10 dan arraySize adalah 13, maka Ia aka...
Read more